Puzzle 中的數學 -1
有一個數學謎題是這樣的:『有七個瓶子放在桌上, 其中四個是正的, 三個是倒的, 現在請你每次調整兩個瓶子(把正的弄倒或是把倒的弄正), 請問要幾次才能讓所有的瓶子是正的。』
答案是 – 永遠沒辦法, 因為瓶子的數量是奇數, 而開始時放正的瓶子是偶數, 每次調整兩個的狀況下。若是兩個都由正變倒, 則正的數量+2; 若兩個都由倒變正, 則正的數量-2; 若一個由倒變正, 一個由正變倒, 則正的數量不變, 也就是不管怎麼動, 永遠都是偶數, 因此沒法達成題目的要求。
在 WSC 2008 的題目中, 也很有趣地有著類似地思維。
(題目圖檔來源: WSC 2008 , Joky 修改)
今年的數獨賽題目類型沒有去年來得多, 但是經過整理, 每回合都有一個主題。而最讓小弟欣賞的則是第七回合的 TWINS 成對題目。同時兩個盤面, 又彼此有邏輯關係, 感覺上更好玩了, 只可惜 Booklet 中的示範沒有題目只有答案, 沒法一償享受解謎的夢想。
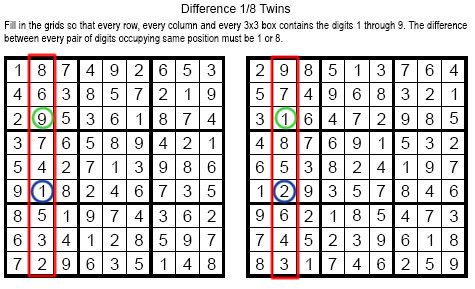
其中在這回合的第一題, Difference 1/8 Twins, 題目的說明如下:『在每行, 每列以及每個3x3 的區域中填入數字1-9, 兩個盤面對應的同樣位子的格子, 差距不是1就是8』
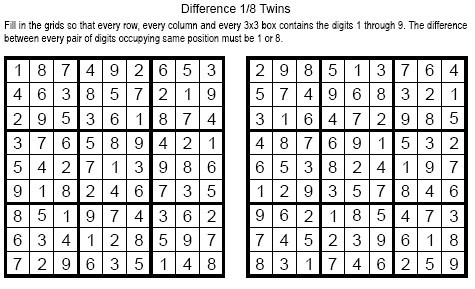
讓我們來想想從規則可以推出什麼技巧, 如果成對的格子差距不是1就是8, 那我們可以假設差距8的格子最多只可能有2組, 最少則是 0 組。因為數字是從1到9, 能差到8 的只有1和9, 也就是兩組(左圖1對到右圖9, 以及左圖9對到右圖1)。當然也可能差距8 的一組都沒有(1對到2, 以及9 對到8)。
但是當我們去看這個答案盤面時, 我們卻發現, 不管是行, 列, 或是 3x3 的區域, 差距8 的格子組都不多不少, 正好是一組, 既沒有兩組的情況, 也不會一組都沒有。所以這是個巧合??還是它真的有另一層原因??
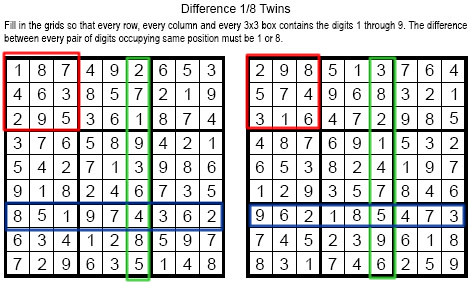
讓我們用瓶子的思維去想這道題目, 為解說方便, 所以拿其中一個3x3 的區域做解釋(同樣道理皆可應用於其他3x3 區域, 行, 及列)。
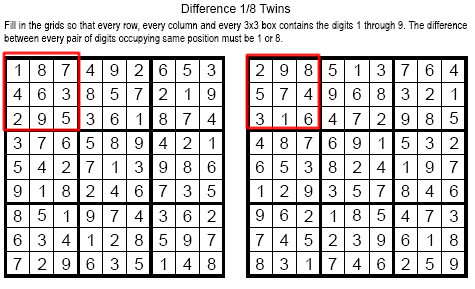
左圖和右圖的區域都是 1-9, 也就是兩圖區域內的總合是相等的。今天假設左右兩圖, 都沒有差距8 的格子組, 那麼它們就一定都是差距 1。那麼左圖格子中的數字, 減掉右圖格子中的數字, 不是 +1就是 -1。而又由於9格的總合相等, 所以差距合計起來應該為0。
你可以試試看用9 個任意的 +1 或 -1 搭配, 看看可不可能湊出零來。答案是不可能, 因為不管怎麼湊都是奇數, 永遠不會是0。
同理, 若左右兩圖, 差距8 的格子組是兩組, 那麼另外七組就是差距1, 當我們拿7 組+1和 -1去湊成0, 會發生和之前一樣無法做到的結果。
也因此, 每行, 列及 3x3 的區域中, 只剩下一組差距 8 的可能性, 而且是唯一可能。
看起來完全沒有關係的瓶子和數獨, 卻在邏輯的思維上, 跨越了數學的天際, 如彩虹般耀眼地, 連繫了彼此。
----
本來想寫到此就好, 不過既然寫了, 就把全部的技巧全部討論完吧!!
每個區域都剛好有一組格子差距 8 , 可以獲得什麼解題技巧??
想當然爾, 若左圖9對應到右圖的 1 , 那麼左圖的 1 就一定是對應到右圖的 2(不能再次差距8), 反之亦然。
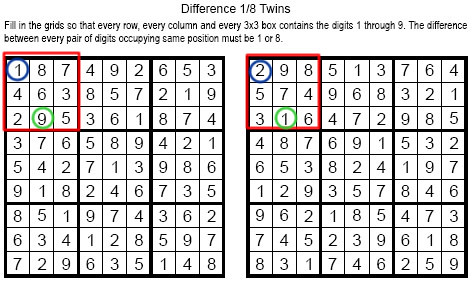
再進一步, 此時右圖的8, 勢必無法再對應左圖的 9(左9已對應到 右1), 一定得對到左圖的 7。
我們再使用總和相同的想法, 左9-右1 = +8, 也就是另外八格一定要總合是-8, 才能夠讓兩區域總和相同, 然而每組格子只能差1, 也就是其他八格 左-右 一定是-1。然後左8對右9, 左7對右8, 左6對右7…以此類推, 到左1對右2。
結束了嗎??還沒有咧…
因為格子所佔的位置, 不只是在區域, 還包括了行及列, 也就是延伸到行列時, 其他的格子都會比照辦理, 左8 對右9, 左7對右8…
而因為要讓行列的總合相同, 所以再對應出去的左9一定又要對到右1(才能有+8 及8個-1相加等於0)的效果。

最後…
只要左右兩圖, 其中一組成對的格子出現, 那我們立刻可判定整個盤面是屬於左-右 為(+8,-1)或(-8,+1), 然後…這道題目不再需要花太多的腦筋, 因為它已經變成國小加減計算題了。
不信的話, 可以再次看看這個盤面, 只要是左9, 一定會對到右1, 而左7也一定都是對到右8, 絕不可能對到右6。其他的數字亦然。這個完全對應的結果既不是巧合, 也不是出題者偷懶省事, 而是個必然的邏輯結果。
現在就只看題目會給多少提示了, 我猜大概不會太多…
希望到時要得到題目:P

回應文章建議規則: